1992年,布爾函數敏感度猜想被提出。這成為了理論計算機科學近三十年來最重要的開放性問題之一。近日,來自Emory大學計算機與數學科學系的華人教授黃皓,用兩頁紙輕鬆證明了困擾理論計算機領域數十年的問題。
組成計算機的電路實際上是「與」「或」「非」邏輯電路的組合,多年來,計算機科學家已經開發出許多方法來測量給定布爾函數的複雜性。
科學家們發現,關於布爾函數的度量措施都適用於一個統一的框架,只有一個複雜性指標似乎不合適:「靈敏度」。1992年,耶路撒冷希伯來大學的Noam Nisan和現在羅格斯大學的Mario Szegedy推測,「靈敏度」的確適合這一框架,但沒人能證明這一點。「我想說,這可能是布爾函數研究中一個懸而未決的問題。」Servedio說。
現在,Emory大學的數學家黃皓用一個巧妙但簡單的兩頁論證,證明了靈敏度猜想,這個論點關於立方體上的點的組合。
法國國家科學研究中心的Claire Mathieu在接受Skype採訪時曾評價它為:「這只是一顆美麗的珍珠。」
黃皓是誰?這位華人科學家是怎麼解開30年來一直困擾計算機科學家的問題呢?
華人數學家——黃皓
黃皓出生於汕頭,這座海濱城市同時也是另一位著名數學家丘成桐的出生地。
十四歲的時候,黃皓就離開家鄉奔赴廣州華南師範大學附屬中學就讀。憑藉優異的成績,2003年黃皓被保送至北京大學攻讀數學專業。在北大就讀時,黃皓就在北京大學舉辦的首屆「江澤涵」杯數學建模與計算機應用競賽中獲得三等獎,並出現在北大數學百年學生名錄上。
2007年北大本科畢業後,黃皓在美國加州大學洛杉磯分校讀博,師從國際著名數學家Benny Sudakov教授,並於2012年獲得博士學位。
曾在2012-2014年受邀訪問美國普林斯頓高等研究院,現擔任美國艾默里大學數學系助理教授。主要研究領域包括極值組合、圖論及計算機理論。

一次偶然與猜想的邂逅
2012年末,在受訪美國普林斯頓高等研究院期間,黃先生在與數學家Michael Saks共進午餐時聽說了敏感性猜想,黃先生是博士後研究員。他立刻被這個猜想的簡潔和優雅所吸引。「從那一刻開始,我開始沉迷於思考它。」他說。
黃將敏感性猜想添加到他感興趣問題的「秘密列表」中,每當他學習新的數學工具時,他都會考慮它是否有幫助。「每次我發表新論文後,我都會回到這個問題,」他說。「當然,我會在一段時間後放棄,並解決一些更現實的問題。」
正如其他研究團體一樣,黃知道,如果數學家可以證明一個關於不同維度立方體上的點集合比較容易陳述的猜想,那麼靈敏度猜想就可以得到解決。從n個0和1的字符串到n維立方體上的點有一種自然的映射關係。
在2013年,黃開始認為理解這個問題的最佳途徑可能是通過標準網絡來表示網絡,該矩陣跟蹤哪些點連接,然後檢查一組稱為矩陣特徵值的數字。五年來,他一直在重新審視這個想法,沒有成功。
「但至少考慮它可以幫助我很快入睡。」他在Aaronson的博客文章中評論道。
然後在2018年,黃髮現了使用一個有200年歷史的稱為Cauchy交錯定理的數學,它將矩陣的特徵值與子矩陣的特徵值聯繫起來,使其成為研究立方體與立方體之間關係的完美工具。黃決定要求國家科學基金會撥款,以進一步探討這一想法。
上個月,當他坐在馬德里的一家酒店寫下他的撥款建議時,他突然意識到他可以通過改變他的矩陣中某些數字的符號來推動這種方法的完成。通過這種方式,他能夠證明在n維立方體中超過一半點的任何集合中,將存在某些與其他點的至少相關的點,靈敏度猜想也從這個結果中被證明。
「美麗的珍珠」
被法國科學家評為「美麗的珍珠」,這一猜想的證明思路是如何實現的呢?
先從「靈敏度」談起,「靈敏度」是一種度量,捕獲輸入字符串中的信息如何影響輸出位改變,換句話說,布爾函數的「靈敏度」跟蹤翻轉單個輸入位改變輸出位的可能性。
舉個例子,想像一下,你正在填寫銀行貸款申請中的一系列Yes/No問題(問卷調查)。完成後,銀行家將對您的結果進行評分,並告訴您是否有資格獲得貸款。這個過程是一個布爾函數:你的答案是輸入位,而銀行家的決定是輸出位。
如果你的申請被拒絕,你可能想知道你是否可以通過單一問題的選擇而銀行的預判結果,比如你口袋裡面真的沒有多少錢時,在收入超過50,000美元那一欄你打了勾,如果這個謊言會導致預判結果,計算機科學家說布爾函數對該特定位的值「敏感」。比方說,如果有七種不同的謊言,你可以說它們會分別翻轉結果,那麼對於你的貸款資料,布爾函數的靈敏度是7。
為了可視化計算機電路對位翻轉錯誤的敏感程度,我們可以將其n個輸入位表示為n維立方體的坐標,例如,四個兩位字符串00,01,10和11對應於二維平面中正方形的四個角:(0,0)、(0,1)、(1,0)和(1,1)。同樣,八個三位字符串對應於三維立方體的八個角,以此類推到更高的維度。反過來,布爾函數可以被認為是用兩種不同顏色著色這些角的規則,如果最終輸出為1則將立方體的一角標為藍色,反之,則標為紅色。

輸入字符串0,1,1的簡單布爾功能可對應到下圖立方體的一角,如果翻轉第一個字符,我們可以發現對「OR」「AND」(或與)電路的輸出沒有什麼影響,相反,如果你翻轉第三位,對於這個操作來說,輸出是敏感的,標記為紅色。
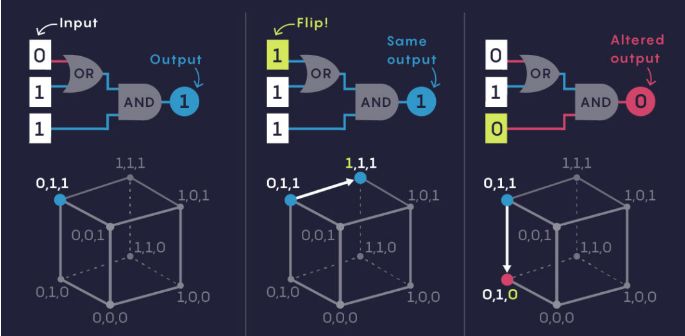
證明靈敏度猜想可以簡化為回答關於不同維度的立方體的簡單問題:如果你選擇任何超過在立方體的一半角落並將它們染成紅色,是否總有一些紅點與許多其他紅點相連?(這裡,通過「連接」,我們的意思是這兩個點共享立方體的一個外邊緣,而不是跨越對角線。)
根據我們的布爾函數對立方體的每個角進行著色。給定輸入字符串的敏感位數由其相關角和另一種不同顏色的角之間的連接數捕獲,電路的整體靈敏度定義為任何輸入字符串中最大位數的敏感位。
下面例子中,點(0,1,1)和(0,0,1)藍紅色點之間的連接,靈敏度為1;點(0,1,1)和(0,1,0)藍紅色點之間的連接,靈敏度為0;點(1,0,1)和(1,0,0)藍紅色點之間的連接,靈敏度為0;點(1,0,1)和(0,0,1)藍紅色點之間的連接,靈敏度為2。
取最大值,因此該布爾函數的靈敏度為2。

靈敏度猜想有什麼用?
證明靈敏度猜想有什麼用呢?
這種猜想可以應用在許多實例中,例如,醫生可能希望在達到診斷之前儘可能少地為患者發送測試,或者機器學習專家可能希望算法在分類之前儘可能少地檢查對象的特徵。
其他措施包括尋找將布爾函數編寫為數學表達式的最簡單方法,或者計算銀行家要向老闆展示多少答案以證明他們已做出正確的貸款決策,其中銀行家可以同時詢問幾個問題的「疊加」;甚至還有量子物理學版本的查詢複雜性,弄清楚該測量與其他複雜性測量的關係如何幫助研究人員理解量子算法的局限性。
黃的結果甚至超過了證明靈敏度猜想所必需的結果,這種發現應該會產生關於複雜性度量的新見解。最重要的是,儘管如此,黃的結果仍然令人擔心,在複雜的世界中,敏感性是否可能是一些奇怪的異常值,還需要後續進一步的研究。