現在,AI不僅能參與數學研究,甚至還快人一步,開始幫助人類提出數學猜想了。
就在今天,這隻由DeepMind與頂級數學家合作研發的AI,登上了最新一期Nature封面。
有多頂級呢?這些數學家全部都來自牛津大學、雪梨大學,其中還不乏英國皇家學會史上最年輕的院士。
就是這位,曾在兩年內斬獲謝瓦萊獎、克雷研究獎等4項數學大獎的Geordie Williamson。
對於這項研究,DeepMind官方自稱其「首次證明了人工智慧可以走在純數學研究的前沿」。
為什麼這次的研究被Nature評價為「AI與人類合作」甚至是「AI指引人類直覺」,與「人類使用AI工具」有何不同?
首先我們要知道,證偽一個猜想相對簡單,只需要找出一個反例即可。
但從零開始提出一個全新猜想這種工作,AI還是首次參與進來。
猜想本身是推動數學發展的一大動力,世界近代三大數學難題都是猜想:費馬猜想、四色猜想和哥德巴赫猜想。

Geordie Williamson
此前提出猜想主要靠少數科學家的洞察力和個人經驗積累,比如歷史上兩位天才,物理學家愛因斯坦和數學家拉馬努金。
但隨著科學不斷發展,需要研究的問題複雜程度逐漸超出人類能力極限。
有的問題涉及的數據規模,是一個人一輩子也研究不完的。
有的研究對象複雜程度之高,甚至可以有幾千個維度,超出了一般人類大腦從直覺上可以理解的能力。
除此之外,這次研究也幫忙搞了搞數學領域記憶體在了40年的陳年老題,得到了不小進展。
參與這次研究的數學家之一,牛津大學的Marc Lackenby說:
我很震驚機器學習在直覺指引上的作用這麼大,也沒想到我過去先入為主的一些觀念被AI給顛覆了。
沒有參與這次研究的另一位數學家,以色列特拉維夫大學的Adam Zsolt Wagner也很羨慕:
如果沒有這個工具,我們數學工作者可能會花上數周至數月的時間,最終發現證明的公式或定理是錯誤的。」
那麼,AI這次到底幫助數學家們解決了哪些問題?下面來一探究竟。
AI發現代數和幾何間的聯繫
第一個問題關於紐結理論(Knot Theory),是拓撲學的一個分支。
用數學語言來講,紐結是一個圓在三維實歐氏空間中的嵌入。
呃……還是看圖吧。
假設你有一根繩子,打上一個結。

再把兩端粘起來,這就是一個紐結(Knot)了。

結可以多打幾個,比如這樣:

或者,這樣?

數學家倒是不關心紐結到底是用鞋帶還是麵包做的,他們最關心一件事:
一個複雜的紐結能不能被還原成簡單的紐結,如果能就說明這兩種紐結在拓撲上是等價的。

以此為依據給紐結分類,才能理解它們的性質,進一步與實際應用問題建立聯繫。
紐結理論在現實世界中,可以用來確定一個化學分子是否有手性,還有希望靠拓撲量子計算模型構建出量子計算機。
數學家們從幾何特徵和代數特徵兩個角度去研究紐結,分別定義了紐結的幾個屬性。

但問題難就難在紐結的種類太多,自19世紀以來人類已經收集了無數種,如果用上計算機自動生成,現在每天都能生成幾十億種。
普通人難以從海量數據中發現隱藏的模式,AI這次卻做到了。
AI的貢獻是發現了紐結的幾何特徵和代數特徵之間存在直接的關聯。
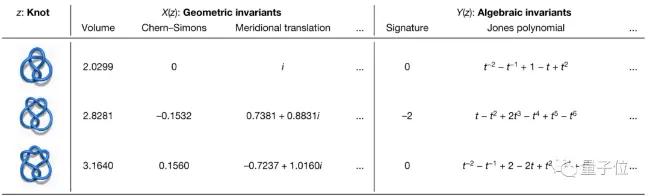
數學家由此發現提出猜想,再給出嚴格證明,為紐結問題研究開闢了新的方向。
40年難題終於有望得證
除了解決了扭結問題之外,另一個則與表示論(Representation theory)相關。
表示論是數學中抽象代數的一支,表示的所有構件都不可約。
而這種不可約表示(Irreducible representations)的結構主要受Kazhdan-Lusztig(KL)多項式的影響。
組合不變性猜想(Combinatorial Invariance Conjecture)就是與KL多項式相關的一個重要猜想。
它指出,對稱群SN中兩個元素的KL多項式可以從它們的無標記Bruhat區間,即一個有向圖中計算出來:
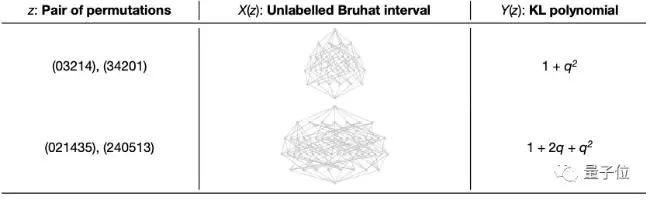
△Bruhat區間及其KL多項式的例子
這一猜想已經存在了40年,卻只有部分進展。
兩位科學家將這個猜想作為初始假設,通過AI中的監督學習模型從Bruhat區間預測KL多項式。
通過計算與確定的歸因技術(Attribution Techniques)相關的代表性子圖,並分析這些圖與原始圖的邊緣分布,他們發現了進一步的結構證據:
如下圖,KL多項式可以通過一個公式直接從超立方體和SN-1部分計算出來。

因此,科學家們提出猜想:
一個無標記的Bruhat區間的KL多項式可以用上述的方法,並通過任何超立方體分解(hypercube decomposition)進行計算。
雖然還沒有進行嚴格證明,但目前他們已能在300萬個測試例子上驗證這一方法。
如果驗證成立,那麼對稱群(Symmetric Group)的組合不變性猜想問題將得到解決。
AI引導數學家直覺
那麼整體來說,數學家們到底是怎麼與AI合作解決問題的?
或者說AI到底是如何幫助引導數學家的直覺的呢?
簡單來說,這篇論文中提出了一種框架,用來快速驗證對兩個量之間關係的猜想(直覺)是否值得繼續探索,如果是的話,則指導如何進一步研究。
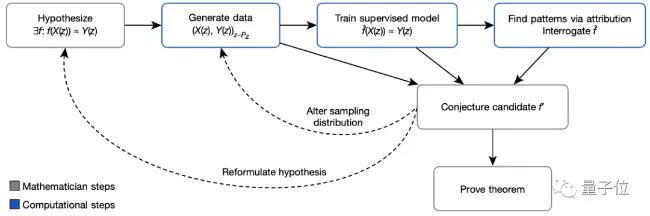
△框架流程圖
具體的,先通過監督學習來驗證數學對象中的某一結構/模式的假設是存在的。
然後,再使用歸因技術來深入理解這些模式。
在這個過程中,AI能夠以人類無法比擬的規模輸出數據,並從數據中挑選出人類無法檢測到的模式。
這正是AI和人類合作與傳統的數學研究方法的不同。
其實,數學在很大程度上是一門對關係和模式進行研究的學科。
比如我們小學時就學過的勾股定理,如果將平面上的三角形擴展到八維空間中的900邊多面體,還能輕易找到a2+b2=c2的等價形式嗎?
答案是:數學家們可以找到,但他們能做的工作量有限。
因為一個人必須評估許多例子,然後才能確定觀察到的公式是普遍通用而非偶然。
當然,這篇論文也並不打算創造一個「通用的純數學助手」,而是讓AI去幫助數學家更有效地發現和識別數學中的新模式。
論文的作者之一,牛津大學的Juhász教授表示:
任何可以生成足夠大數據集的數學領域都可以使用這種方法,而生物、經濟學等領域也將從其中收益。
除了Nature論文外,研究人員還在Arxiv上發布了數學角度解釋兩個研究的論文,將來會投到合適的數學期刊。
另外還為兩個問題提供了Colab代碼,讓你體驗一下與AI合作搞科研是什麼感覺。